Plano Complejo Extendido

Plano Complejo Extendido $\widehat{\mathbb{C}}$

El estudio de las funciones complejas meromorfas nos induce naturalmente a agregar un nuevo punto al plano complejo $\mathbb{C}.$ Dicho punto lo llamamos infinito y lo denotamos con el símbolo $\infty$ Este símbolo fue introducido por el matemático inglés John Wallis (1616-1703), en su obra titulada Trataise of Algebra (Wallis), publicada en 1685.. A este nuevo conjunto $\mathbb{C}\cup\{\infty\}$ lo podemos dotar con una topología, a partir del proceso conocido como la compactación de Alexadrov. Para una descripción del caso general invitamos al lector a consultar Dugundji, 8.4 Theorem, pág. 246.

Consideremos el plano complejo $\mathbb{C}$ con su topologia usual $\tau_{\mu}$ y el infinito $\infty\notin \mathbb{C}.$ Definimos el conjunto $\widehat{\mathbb{C}}:=\mathbb{C}\cup\{\infty\}$ y la familia \[ \tau_{\infty}:=\tau_{\mu}\cup\{V\subset \widehat{\mathbb{C}}: \widehat{\mathbb{C}}-V \text{ es compacto en } \mathbb{C}\}. \] Entonces

La pareja $(\widehat{\mathbb{C}}, \tau_{\infty})$ es un espacio topológico compacto y Hausdorff.
La pareja $(\widehat{\mathbb{C}},i)$ es una compactificación de $\mathbb{C},$ donde $i$ es la inclusión.

El espacio topológico $\widehat{\mathbb{C}}$ es llamado:

Plano Complejo Extendido o Esfera de Riemann

Iniciaremos probanado que $\tau_{\infty}$ es una topología en $\widehat{\mathbb{C}}.$ Concretamente, debemos verificar el cumpliento de las tres propiedades para espacios topológico.

Propiedad 1. Evidentemente, $\emptyset \in \tau_{\mu}\subset \tau_{\infty}.$ Por otro lado, $\emptyset=\widehat{\mathbb{C}}\setminus \widehat{\mathbb{C}}$ es compacto en $\mathbb{C},$ por lo tanto $\widehat{\mathbb{C}}\in \tau_{\infty}.$

Propiedad 2. Tomemos los elementos $U_{1}$ y $U_{2}$ en $\tau_{\infty}.$ Verifiquemos que la intersección $U_{1}\cap U_{2}$ está en $\tau_{\infty}.$ Debemos estudiar tres casos.

Caso 1. Si $\infty\in U_{1}\cap U_{2},$ entonces las diferencias $\widehat{\mathbb{C}}\setminus U_{1}$ y $\widehat{\mathbb{C}}\setminus U_{2}$ son subconjuntos compactos de $\mathbb{C}.$ Dado que la unión finita de compactos es un compacto, entonces $(\widehat{\mathbb{C}}\setminus U_{1})\cup (\widehat{\mathbb{C}}\setminus U_{2})$ es un subconjunto compacto de $\mathbb{C}.$ Aplicando las leyes de Morgan al anterior conjunto, tenemos que

\[ (\widehat{\mathbb{C}}\setminus U_{1})\cup (\widehat{\mathbb{C}}\setminus U_{2})=\widehat{\mathbb{C}}\setminus (U_{1}\cap U_{2}). \]

De esta última igualdad, concluimos que $U_{1}\cap U_{2}\in \tau_{\infty}.$

Caso 2. Si $\infty\in U_{1}\cap U_{2},$ entonces las diferencias $\widehat{\mathbb{C}}\setminus U_{1}$ y $\widehat{\mathbb{C}}\setminus U_{2}$ son subconjuntos compactos de $\mathbb{C}.$ Dado que la unión finita de compactos es un compacto, entonces $(\widehat{\mathbb{C}}\setminus U_{1})\cup (\widehat{\mathbb{C}}\setminus U_{2})$ es un subconjunto compacto de $\mathbb{C}.$ Aplicando las leyes de Morgan al anterior conjunto, tenemos que

\[ (\widehat{\mathbb{C}}\setminus U_{1})\cup (\widehat{\mathbb{C}}\setminus U_{2})=\widehat{\mathbb{C}}\setminus (U_{1}\cap U_{2}). \]

De esta última igualdad, concluimos que $U_{1}\cap U_{2}\in \tau_{\infty}.$

Caso 3. Si $\infty\in U_{1}$ y $U_{2}\in\tau_{\infty}.$ Entonces $\infty \notin U_{1}\cap U_{2}.$ El conjunto intersección anterior lo reescribimos de la siguiente manera

\begin{equation} \begin{split} U_{1}\cap U_{2}&=(U_{1}\setminus \{\infty\})\cap U_{2},\\ &=(\mathbb{C}\cap U_{1})\cap U_{2},\\ &=\left(\mathbb{C}\setminus \left(\widehat{\mathbb{C}}\setminus U_{1}\right)\right)\cap U_{2}.\\ \end{split} \end{equation}

Dado que $\widehat{\mathbb{C}}\setminus U_{1}$ es un subconjunto compacto de $\mathbb{C},$ entonces $\mathbb{C}\setminus \left(\widehat{\mathbb{C}}\setminus U_{1}\right)$ es un abierto de $\tau_{\mu}.$ Por lo tanto, $U_{1}\cap U_{2}\in \tau_{\mu}\subset \tau_{\infty}.$

Propiedad 3. Tomemos la familia $\{U_{i}\in \tau_{\infty}:i\in I\}$ y veamos que $\bigcup\limits_{i\in I}U_{i}\in \tau_{\infty}.$ Si $U_{i}\in \tau_{\mu}$ para todo $i\in I,$ usamos el hecho que $\tau_{\mu}$ es una topología y concluimos que $\bigcup\limits_{i\in I}U_{i}\in \tau_{\mu}\subset \tau_{\infty}.$ Por otro lado, si existe $j'\in I,$ tal que $\infty\in U_{j'},$ entonces consideramos el conjunto de índices $J=\{j\in I: \infty \in U_{j}\}.$ Entonces el conjunto unión $\bigcup\limits_{i\in I}U_{i}$ lo reescribimos como sigue

\[ \bigcup_{i\in I}U_{i}=\left(\bigcup_{j\in J}U_{i}\right)\cup \left(\bigcup\limits_{i\in I\setminus J}U_{i}\right). \]

Tomamos complementos en la anterior igualdad y aplicamos leyes de Morgan. Así, obtenemos

\begin{equation}\label{eq:t_plano_complejo_extendido_1} \begin{split} \hat{\mathbb{C}}\setminus \bigcup_{i\in I}U_{i}&=\bigcap_{i\in I} (\hat{\mathbb{C}}\setminus U_{i}),\\ &=\left(\bigcap_{j\in J}(\hat{\mathbb{C}}\setminus U_{i})\right)\cap \left(\bigcap\limits_{i\in I\setminus J}(\hat{\mathbb{C}}\setminus U_{i})\right),\\ \end{split} \end{equation}

Notemos que $$\bigcap\limits_{j\in J}(\hat{\mathbb{C}}\setminus U_{i})$$ es un subconjunto compacto y cerrado de $\mathbb{C}.$ Además, $$\bigcap\limits_{i\in I\setminus J}(\hat{\mathbb{C}}\setminus U_{i})$$ es un subconjunto cerrado de $\mathbb{C}.$ Por lo tanto, el conjunto diferencia de la ecuación \eqref{eq:t_plano_complejo_extendido_1} es un subconjunto cerrado. Dado que todo subconjunto cerrado de un compacto y es compacto, entonces concluimos que la diferencia

$$ \hat{\mathbb{C}}\setminus \bigcup\limits_{i\in I}U_{i}\subset \bigcap\limits_{j\in J}(\hat{\mathbb{C}}\setminus U_{i}), $$

es un subconjunto compacto de $\mathbb{C}.$ Por lo tanto, $\bigcup\limits_{i\in I}U_{i}\in \tau_{\infty}.$

Verifiquemos que $\widehat{\mathbb{C}}$ es un espacio Hausdorf. Tomemos los puntos $z\neq w\in\widehat{\mathbb{C}}.$ Si ambos puntos están en $\mathbb{C},$ entonces existen abiertos $U,V\in \tau_{\mu}\subset \tau_{\infty},$ tal que $z\in U,$ $w\in V$ y $U\cap V=\emptyset.$ Por otro lado, si $w=\infty,$ entonces consideramos los reales positivos $0\lt r_{1}\lt r_{2}.$ Luego, constuirmos las bolas abiertas $B_{r_{1}}(z)$ y $B_{r_{2}}(z)$ las cuales están en $\tau_{\mu}.$ Nótese que la cerradura $\overline{B_{r_{2}}(z)}$ de la bola $B_{r_{2}}(z)$ es un compacto de $\mathbb{C}$ y su complemento $V=\widehat{\mathbb{C}}\setminus \overline{B_{r_{2}}(z)}$ en $\widehat{\mathbb{C}}$ es un abierto en $\tau_{\inf}$ que contiene al punto $\infty.$ Por construcción, se tiene que $B_{r_{1}}(z)\cap V =\emptyset.$

Compacidad. Consideremos una cubierta abierta $\mathcal{M}:=\{U_{\alpha}:\alpha \in \mathcal{A}\}$ para $\widehat{\mathbb{C}}.$ Existe un índice $\beta \in \mathcal{A},$ tal que el abierto $U_{\beta}$ contiene el punto $\infty.$ Entonces el conjunto diferencia $B=\widehat{\mathbb{C}}\setminus U_{\beta}$ es compacto en $\mathbb{C}.$ Dado que $B$ es compacto, existe una cantidad finita de abiertos $U_{1},\ldots, U_{n}$ en $\mathcal{M}$ cubriendo a $B,$ para algún $n\in \mathbb{N},$ i.e., $B=\bigcup\limits_{i=1}^{n}U_{i}.$ La familia $\{U_{i},U_{\beta}: i\in\{1,\ldots,n\}\}$ es una cubierta abierta finita tomada de $\mathcal{M},$ la cual cubre a $\widehat{\mathbb{C}}.$

La afirmación descrita en el inciso (ii) se deja como ejercicio al lector.

En el curso de análisis complejo se suele estudiar el concepto de sucesión convergente con el objetivo de entender la continuidad de funciones complejo valuadas. La sucesión de números complejos $(z_{n})_{n\in\mathbb{N}}$ converge a $w\in\mathbb{C},$ si para cada real positivo $ \varepsilon>0$ existe un número natural $N_{\varepsilon}\in\mathbb{N}$ tal que si $m\geq N_{\varepsilon}$ entonces se cumple que $\vert w-z_{m}\vert \lt \varepsilon.$ Equivalentemente, para cada real positivo $\varepsilon>0,$ existe un natural $N_\varepsilon\in\mathbb{N}$ tal que para todo $n\geq N_{\varepsilon}$ el punto $z_{n}$ está en la bola abierta euclidiana $B_{\varepsilon}(w)=\{z\in\mathbb{C}:\vert w-z\vert\lt\varepsilon\}.$ Nuestra intención ahora es extender este concepto al caso del plano complejo extendido. Más precisamente, conocer el siginificado de la convergencia de una sucesión $(z_{n})_{n\in\mathbb{N}}$ al punto $\infty.$ Para tal caso, es conveniente introducir el siguiente abierto. Para todo real $\varepsilon> 0,$ la bola euclidiana cerrada $\overline{B_{\varepsilon}(\textbf{0})}=\{z\in\mathbb{C}: \vert z \vert \leq \varepsilon\}$ es un subconjunto compacto de $\mathbb{C},$ entonces de la definición de la topología $\tau_{\infty}$ se sigue que el conjunto \begin{equation}\label{eq:bola_centro_infinito} B_{\varepsilon}(\infty):=\{z\in\mathbb{C}: |z|>\varepsilon\}\cup\{\infty\}, \end{equation} es una vecindad que contiene al punto $\infty.$ La siguiente definición ayuda a verificar la continuidad de funciones en el punto infinito.

Diremos que la sucesión $(z_n)_{n\in\mathbb{N}}$ conformada por números complejos convergente al punto $\infty,$ si cada real positivo $\varepsilon> 0$ existe un número natural $N_{\varepsilon}\in\mathbb{N}$ tal que si $m\geq N_{\varepsilon},$ entonces $z_n\in B_{\varepsilon}(\infty).$ Equivalentemente, si para cada real positivo $\varepsilon > 0$ existe un número natural $N_{\varepsilon}\in\mathbb{N}$ tal que si $m\geq N_{\varepsilon},$ entonces $|z_m|>\varepsilon.$ Nosotros escribimos \[ \lim\limits_{n\in\mathbb{N}}z_{n}=\infty, \] para expresar que la sucesión $(z_{n})_{n\in\mathbb{N}}$ converge a infinito.

La función conjugada $f:\widehat{\mathbb{C}}\to\widehat{\mathbb{C}}$ definida mediante \begin{equation}\label{eq:funcion_conjugada} f(z)= \left\{ \begin{array}{ ll } \overline{z}; & \text{ si } z\in \mathbb{C}; \\ \infty; & \text{ si } z=\infty;\\ \end{array} \right. \end{equation} es continua en el punto $\infty.$

Si consideramos la sucesión de números complejos $(z_{n})_{n\in\mathbb{N}}$ convergente a $\infty,$ debemos verificar que la sucesión $(\overline{z}_{n})_{n\in\mathbb{N}}$ converge a $\infty.$ Por hipótesis, dado el real positivo $\varepsilon>0$ existe un número natural $N_{\varepsilon}\in\mathbb{N}$ tal que si $m\geq N_{\varepsilon},$ entonces $\vert z_{m}\vert > \varepsilon.$ De las propiedades del conjugado se sabe que $\vert z \vert = \vert \overline{z}\vert,$ para todo $z\in\mathbb{C},$ entonces para todo $m\geq N_{\varepsilon}$ se cumple $\vert \overline{z}_{m}\vert=\vert z_{m}\vert > \varepsilon.$

Proyección Estereográfica

Desde el punto de vista histórico, los griegos entendieron el plano complejo extendido como un objeto geométrico, más precisamente como la esfera unitaria

\[ \mathbb{S}^{2}:=\left\{(x_1,x_2,x_3)\in\mathbb{R}^3: x_1^2+x_2^2+x_3^2=1\right\}. \]

En la obra Planisphaerium, su autor, Claudio Ptolomeo, describió una función proyección (proyección estereográfica) desde la esfera celestial hasta el plano euclidiano, la cual envía la parte celestial del polo norte (cuya frontera es el gran cíarculo invisible) sobre el interior de una circunferencia del plano euclidiano (véase Berggren). ¡Vamos a introducir esta proyección!

El número complejo $z=x_{1}+ix_{2}$ lo identificamos con la tripleta $(x_{1},x_{2},0),$ esta asociación nos permite pensar el plano complejo $\mathbb{C}$ como el plano

$$P=\{(x_1,x_2,x_3)\in\mathbb{R}^3: x_3=0\}.$$

La tripleta ${\rm N}=(0,0,1)$ sobre la esfera $\mathbb{S}^{2}$ es llamada el polo norte. Entonces para todo un punto $\textbf{x}=(x_1,x_2,x_3)$ sobre $\mathbb{S}^{2}-\{\rm N\},$ existe una única línea recta $\ell_{\textbf{x}}$ que pasa por los puntos $\textbf{x}$ y ${\rm N}.$ La línea recta $\ell_{\textbf{x}}$ intersecta al plano $ P$ en un único punto $z$ (véase Figura 1). Entonces definimos la correspondencia $\Pi,$ la cual asocia al punto $\textbf{x}\in \mathbb{S}^2-\{\rm N\}$ el complejo $z$ que está en la intersección de la línea recta $\ell_{\textbf{x}}$ y el plano $ P.$ Además, $\Pi$ envía el polo norte ${\rm N}$ sobre el punto infinito $\infty.$

Proyección estereográfica: Mueve el punto $z.$ Con el mouse puedes mover la vista en 2D y 3D. También puedes hacer Zoom In o Out.

La función $\Pi: \mathbb{S}^{2}\to \widehat{\mathbb{C}},$ tal que

\begin{equation}\label{eq:proyeccion_esterografica} \Pi(\textbf{x})= \left\{ \begin{array}{ ll } \ell_{\textbf{x}}\cap P; & \text{ si } \textbf{x}\neq {\rm N}; \\ \infty; & \text{ si } \textbf{x}={\rm N};\\ \end{array} \right. \end{equation}

es llamada la proyección estereográfica.

Ahora vamos a dar un descripción más precisa de la regla de asignación $\Pi(\textbf{x}).$ Si fijamos la tripleta $\textbf{x}=(x_1,x_2,x_3)$ sobre $\mathbb{S}^2-\{ {\rm N}\},$ entonces queremos encontrar explícitamente el complejo $z$ en l a intersección $\ell_{\textbf{x}}\cap P.$ La línea recta $\ell_{\textbf{x}}$ está conformada por las tripletas $(\overline{x}_1,\overline{x}_2,\overline{x}_3)\in\mathbb{R}^2$ que satisfacen la ecuación

\[ (\overline{x}_1,\overline{x}_2,\overline{x}_3)=t(x_1,x_2,x_3-1)+(0,0,1), \text{ para cada } t\in\mathbb{R}. \]

Equivalentemente, para cada $t\in \mathbb{R}$ se cumplen las siguientes ecuaciones paramétricas

\begin{equation}\label{eq:valor_t} \overline{x}_1=tx_1, \quad \overline{x}_2 =tx_2, \quad \overline{x}_3 =t(x_3-1)+1. \end{equation}

Nuestro objetivo es encontrar la tripleta $(\overline{x}_1,\overline{x}_2,\overline{x}_3)$ sobre la línea recta $\ell_{\textbf{x}}$ tal que $\overline{x}_{3}=0,$ lo cual significa obtener el real $t\in\mathbb{R}$ tal que $\overline{x}_3=0.$ De la tercera relación descrita en la ecuación \eqref{eq:valor_t}, deducimos fácilamente que la igualdad $\overline{x}_3=0$ sucede cuando $$ t=\dfrac{1}{1-x_3}. $$ Sustituimos el valor encontrado de $t$ en las dos primeras igualdades de la ecuación (\ref{eq:valor_t}) y obtenemos

\[ \overline{x}_1=\frac{x_1}{1-x_3}, \quad \overline{x}_2=\frac{x_2}{1-x_3}. \]

Entonces el punto de intersección entre la línea $\ell_{\textbf{x}}$ y el plano $P$ es el complejo

$$ \dfrac{x_1}{1-x_3}+i\dfrac{x_2}{1-x_3}. $$

Entonces la proyección estereográfica (\ref{eq:proyeccion_esterografica}) está definida mediante

\begin{equation}\label{eq:proyeccion_esteregrafica_2} \Pi(x_1,x_2,x_3)= \left\{ \begin{array}{ cl } \dfrac{x_1}{1-x_3}+i\dfrac{x_2}{1-x_3}; & \text{ si } (x_1,x_2,x_3)\neq {\rm N}; \\ \infty; & \text{ si } (x_1,x_2,x_3)={\rm N}.\\ \end{array} \right. \end{equation}

Naturalmente nos preguntamos ¿cuál es la función inversa $\Pi^{-1}$? ¡Vamos a contestarla!

Si tomamos el complejo $z=x_1+ix_2$ identificado con la tripleta $(x_1,x_2,0)\in\mathbb{R}^3,$ entonces existe una única línea recta $\ell_{z}$ que pasa por $(x_1,x_2,0)$ y el polo norte ${\rm N}.$ La recta $\ell_z$ está conformada por las tripletas $(\overline{x}_1,\overline{x}_2,\overline{x}_3)\in\mathbb{R}$ que satisfacen la ecuación

\begin{equation}\label{eq:linea_recta} \overline{x}_1=tx_1, \quad \overline{x}_2=tx_2, \quad \overline{x}_3=1-t, \text{ para cada } t\in\mathbb{R}. \end{equation}

Queremos encontrar las tripletas $(\overline{x}_1,\overline{x}_2,\overline{x}_3)$ que están sobre la línea recta $\ell_{z}$ tal que $\overline{x}_{1}^2+\overline{x}_{2}^2+\overline{x}_{3}^2=1.$ Reemplazamos en la igualdad anterior las relaciones descritas en (\ref{eq:linea_recta}) y obtenemos \[ (tx_1)^2+(tx_2)^2+(1-t)^2 =1. \] Resolvemos la ecuación de segundo grado,

\begin{equation*} \begin{split} (tx_1)^2+(tx_2)^2+(1-t)^2 & =1,\\ t^2 (x_1^2+x_2^2+1)-2t & =0,\\ t \left[ t(x_1^2+x_2^2+1)-2\right] & =0.\\ \end{split} \end{equation*}

Así, obtenemos

$$t=\dfrac{2}{x_1^2+x_2^2+1}$$

o $t=0.$ Al reemplazar este valor real en la ecuación (\ref{eq:linea_recta}) tenemos que el punto en la intersección de la recta $\ell_{z}$ y el conjunto $\mathbb{S}^{2}-\{\rm N\}$ es la tripleta

\[ \left(\frac{2x_1}{x_2^2+x_2^2+1},\frac{2x_2}{x_2^2+x_2^2+1},\frac{x_1^2+x_2^2-1}{x_2^2+x_2^2+1}\right). \]

La función inversa $\Pi^{-1}$ de la proyección estereográfica está dada por

\begin{equation}\label{eq:proyeccion_estereografica_inversa} \Pi^{-1}(z)= \left\{ \begin{array}{ cl } \left(\dfrac{2x_1}{x_1^2+x_2^2+1},\dfrac{2x_2}{x_1^2+x_2^2+1},\dfrac{x_1^2+x_2^2-1}{x_2^2+x_2^2+1}\right); & \text{ si } z=x_1+ix_2; \\ {\rm N}; & \text{ si } z=\infty.\\ \end{array} \right. \end{equation}

El lector puede verificar que efectivamente se satisfacen las siguientes igualdades de funciones $\Pi^{-1}\circ \Pi={\rm Id}_{\mathbb{S}^2}$ y $\Pi\circ\Pi^{-1}={\rm Id}_{\hat{\mathbb{C}}}.$ Estas dos relaciones implican que ambas funciones $\Pi$ y $\Pi^{-1}$ son biyectivas. Adicionalmente, puede convencerse fácilmente que la proyección estereográfica envía el círculo ecuatorial de $\mathbb{S}^2$ (la intersección de $\mathbb{S}^2$ con el plano $xy$) en la circunferencia euclidiana con centro en $\textbf{0}$ y radio $1$ (véase Figura 1). Incluso más, la proyección $\Pi$ envía círculos de las esfera sobre círculos del plano complejo extendido. Este hecho es conocidos desde hace tiempo, en la obra De plana spera escrita por Jordanus Nemorarius, el autor trató los principios de la proyección esterográfica y probó que la proyección envía círculos de la esfera $\mathbb{S}^2$ en círculos del plano complejo extendido Folkerts & Lorch (2007, p. 6). Vamos a introducir el concepto de círculo en el plano complejo extendido y probar esta propiedad de la proyección estereográfica.

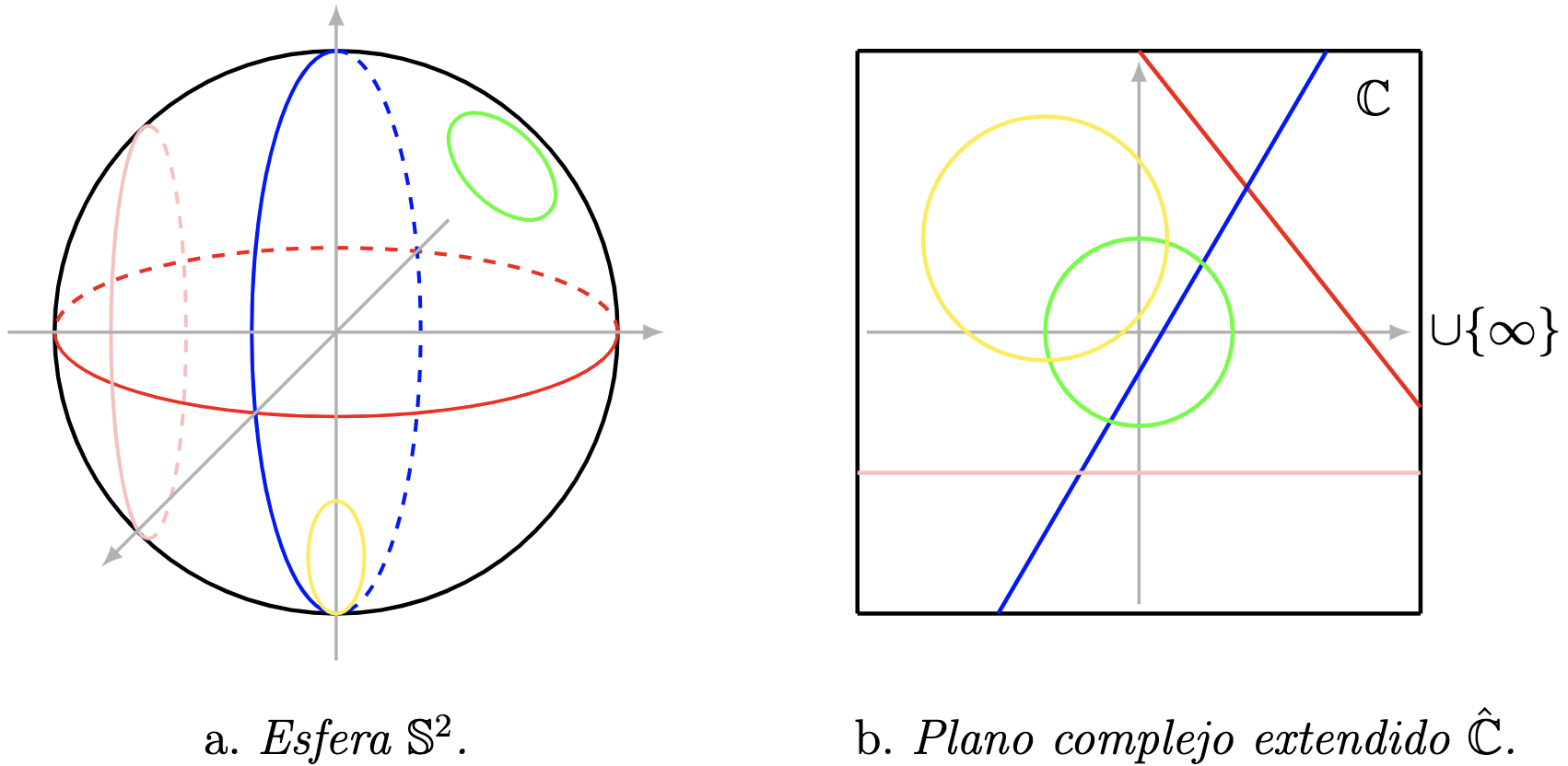
Un círculo sobre la esfera $\mathbb{S}^2$ es el conjunto con más de un punto que se obtiene de la intersección de un plano $P'$ y la esfera $\mathbb{S}^{2}$ (véase Figura 2-a). Un círculo generalizado sobre el plano complejo extendido $\widehat{\mathbb{C}}$ es una circunferencia euclidiana en $\mathbb{C}$ o, una línea recta euclidiana en $\mathbb{C}$ junto con el punto $\infty$ (véase Figura 2-b).

La proyección esterográfica envía círculos de la esfera unitaria $\mathbb{S}^2$ sobre círculos generalizados del plano complejo extendido $\widehat{\mathbb{C}}.$ Además, la imagen inversa de cualquier círculo generalizado bajo la proyección estereográfica es un círculo en la esfera unitaria.

Dados los números reales $a,b,c,d\in\mathbb{R},$ consideramos el círculo $C$ sobre la esfera unitaria $\mathbb{S}^{2},$ donde

\begin{equation}\label{eq:plano_circunferencia} C=\left\{(\overline{x}_1,\overline{x}_2,\overline{x}_3)\in \mathbb{S}^{2}: a\overline{x}_1+b\overline{x}_2+c\overline{x}_3=d\right\}. \end{equation}

Veamos que la imagen $\Pi(C)$ es un círculo generalizado sobre el plano complejo extendido $\widehat{\mathbb{C}},$ es decir,

\[ \Pi(C)=\left\{x_{1}+ix_{2}\in\mathbb{C}: \tilde{a}(x_1^2+x_2^{2})+2\tilde{b}x_1+2\tilde{c}x_2+\tilde{d}=0 \right\}, \]

para reales adecuados $\tilde{a},\tilde{b},\tilde{c},\tilde{d}\in\mathbb{R}.$ Al conjunto anterior le agregamos el punto $\infty,$ si el círculo $C$ pasa por el polo norte ${\rm N}.$

Como la proyección estereográfica $\Pi$ es una biyección y $C$ tiene más de un punto, entonces de la relación \eqref{eq:proyeccion_estereografica_inversa} se sigue que existe un número complejo $x_{1}+i x_{2}$ tal que

\[ (\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})=\left(\dfrac{2 x_1}{x_1^2+x_2^2+1},\dfrac{2 x_2}{x_1^2+x_2^2+1},\dfrac{x_1^2+x_2^2-1}{x_2^2+x_2^2+1}\right). \]

Reemplazamos la anterior igualdad en la ecuación (\ref{eq:plano_circunferencia}) y obtenemos

\[ a\left(\frac{2x_1}{x_2^2+x_2^2+1}\right) +b\left(\frac{2x_2}{x_1^2+x_2^2+1}\right)+c\left(\frac{x_1^2+x_2^2-1}{x_1^2+x_2^2+1}\right) =d. \]

Finalmente, realizamos operaciones básicas y llegamos a la expresión

\begin{equation}\label{eq:final_circunferencia_bajo_proyeccion} \begin{split} 2ax_1 +2bx_2+c\left(x_1^2+x_2^2-1\right)& =d(x_1^2+x_2^2+1),\\ (c-d)x_1^2+(c-d)x^2_2 +2ax_1 +2bx_2&=d+c.\\ \end{split} \end{equation}

Entonces la imagen $\Pi(C)$ está descrita de la forma

\begin{equation}\label{eq:imagen_circulo_proyeccion_estereografica} \Pi(C)=\left\{x_{1}+ix_{2}\in\mathbb{C}: (c-d)x_1^2+(c-d)x^2_2 +2ax_1 +2bx_2=d+c\right\}. \end{equation}

Debemos estudiar los siguientes dos casos.

Caso 1. Si $c-d=0,$ entonces la ecuación \eqref{eq:final_circunferencia_bajo_proyeccion} se reescribe como \[ 2ax_{1}+2bx_{2}=d+c. \] Esta última expresión representa una línea recta euclidiana. Entonces la imagen

\[ \Pi(C)=\left\{(x_{1},x_{2})\in\mathbb{R}^2: 2ax_1+2bx_2=d+c \right\}\cup\{\infty\}, \]

es un círculo generalizado.

Caso 2. Contrariamente, si $c-d\neq 0,$ entonces dividimos entre $c-d$ la ecuación \eqref{eq:final_circunferencia_bajo_proyeccion}, luego completamos cuadrados y obtenemos

\begin{equation}\label{eq:proyeccion_circulos_en_circulos} \small{\begin{split} x_1^2+\frac{2a}{(c-d)}x_1 +\frac{a^2}{(c-d)^2} +x_2^2+\frac{2b}{(c-d)}x_2^2+\frac{b^2}{(c-d)^2}&=\frac{d+c}{c-d}+\frac{a^2}{(c-d)^2}+\frac{b^2}{(c-d)^2}\\ \left(x_1^2+\frac{a}{c-d}\right) +\left(x_2^2+\frac{b}{c-d}\right)&=\frac{a^2+b^2+c^2-d^2}{(c-d)^2}.\\ \end{split}} \end{equation}

Debemos verificar que $a^{2}+b^{2}+c^{2}-d^{2}>0.$ Si el plano $P$ dado por la fórmula \[ a\overline{x}_1+b\overline{x}_2+c\overline{x}_3=d, \] pasa por el origen $\textbf{0},$ entonces $d=0$ y así, el miembro derecho de la expresión en \eqref{eq:proyeccion_circulos_en_circulos} debe ser un real positivo.

Por otro lado, la distancia $D$ desde un punto arbitrario $(x_{0},y_{0},z_{0})\in\mathbb{R}^{3}$ hasta el plano $P$ con ecuación $ax_{1}+bx_{2}+cx_{3}=d,$ es \[ D=\dfrac{|ax_{0}+by_{0}+cz_{0}-d|}{\sqrt{a^{2}+b^{2}+c^{2}}}. \] Si el plano $P,$ descrito anteriormente, no pasa por el origen $\textbf{0},$ entonces la distancia de dicho plano $P$ al origen $\textbf{0}$ es \[ 1>D=\dfrac{|-d|}{\sqrt{a^{2}+b^{2}+c^{2}}}>0. \] Aplicando operaciones básicas a esta última desigualdad, obtenemos $a^{2}+b^{2}+c^{2}-d^{2}>0.$

Ahora, vamos a demostrar la segunda afirmación del teorema. Tomemos un círculo generalizado $C$ sobre el plano complejo extendido $\widehat{\mathbb{C}}.$ Probemos que la imagen inversa $\Pi^{-1}(C)$ es una circunferencia sobre $\mathbb{S}^2,$ es decir,

\[ \Pi^{-1}(C)=\left\{(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})\in\mathbb{S}^2: a\overline{x}_{1}+b\overline{x}_{2}+c\overline{x}_{3}=d\right\}, \]

para algunos reales $a,b,c,d\in\mathbb{R}.$

La circunferencia generalizada $C$ en el plano complejo extendido $\hat{\mathbb{C}}$ está dada por

\begin{equation}\label{eq:general_circulo_1} C=\left\{ x_{1}+ix_{2}\in\mathbb{C}: a(x_{1}^{2}+x_{2}^{2})+2bx_{1}+2cx_{2}+d=0\right\}, \end{equation}

siendo $a,b,c,d$ reales adecuados. De la relación \eqref{eq:proyeccion_esteregrafica_2} existe una tripleta $(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})\in \Pi^{-1}(C)$ tal que

\[ x_{1}=\frac{\overline{x}_{1}}{1-\overline{x}_{3}} \text{ y } x_{2}=\frac{\overline{x}_{2}}{1-\overline{x}_{3}}. \]

Sustituimos las anteriores relaciones en la igualdad \eqref{eq:general_circulo_1} y obtenemos

\begin{equation}\label{eq:plano_esfera_unitaria} \Pi^{-1}(C)=\left\{(\overline{x}_{1},\overline{x}_{2},\overline{x}_{2})\in\mathbb{S}^{2}: F(\overline{x}_{1},\overline{x}_{2},\overline{x}_{2})=0\right\}. \end{equation}

donde

\[ F(\overline{x}_{1},\overline{x}_{2},\overline{x}_{2})=a\frac{(\overline{x}_{1}^{2}+\overline{x}_{2}^{2})}{(1-\overline{x}_{3})^2}+2b\frac{\overline{x}_{1}}{1-\overline{x}_{3}}+2c\frac{\overline{x}_{2}}{1-\overline{x}_{3}}+d. \]

Recordemos que la tripleta $(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})\in\mathbb{S}^2$ satisface la relación $\overline{x}_{1}^{2}+\overline{x}_{2}^{2}+\overline{x}_{3}^{2}=1.$ Equivalentemente, se cumple la igualdad $\overline{x}_{1}^{2}+\overline{x}_{2}^{2}=1-\overline{x}_{3}^{2}.$ Reemplazamos esta última igualdad en la ecuación \eqref{eq:plano_esfera_unitaria}, computamos y obtenemos

\[ \Pi^{-1}(C)=\left\{(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})\in\mathbb{S}^2: a(1+\overline{x}_3)+2b\overline{x}_1+2c\overline{x}_{2}+d(1-\overline{x}_{3})=0\right\}. \]

La proyección esterográfica $\Pi$ es un homeomorfismo.

Verificar que la proyección estereográfica es una biyección es rutina, se deja como ejercicio al lector. Comenzaremos probando que la proyección estereográfica $\Pi$ es continua. Recordemos que la $i$-ésima proyección $p_{i}:\mathbb{C}\to\mathbb{R},$ es continua, para cada $i\in\{1,2\}.$ Nótemos que la composición $$ p_{i}\circ \Pi(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})=\frac{\overline{x}_{i}}{1-\overline{x}_{3}}, $$ es continua en cada tripleta $(\overline{x}_{1},\overline{x}_{2},\overline{x}_{3})\in\mathbb{S}^2-\{\rm N\}.$

Usando la Proposición en Rosenlicht, (1986, pág. 77) concluimos que la proyección estereográfica $\Pi$ es continua en $\mathbb{S}^2\setminus\{\rm N\}.$ Ahora, probemos la continuidad de $\Pi$ en el punto $\infty.$ Consideremos el subconjunto abierto $V\subset \widehat{\mathbb{C}}$ que contiene a $\Pi({\rm N})=\infty.$ Veamos que existe un abierto $W$ que contiene al polo norte ${\rm N}$ tal que $\Pi(W)\subset V.$ Por la manera en que se definió la topología $\tau_{\infty}$ para $\widehat{\mathbb{C}}$ (véase Teorema 1), se sigue que $\widehat{\mathbb{C}}-V$ es un subconjunto compacto de $\mathbb{C}.$ Entonces existe un real positivo $r>0,$ el compacto $(\widehat{\mathbb{C}}-V)$ se queda contenido en la bola euclidiana $B_{r}(\textbf{0}).$ Nótemos que la frontera $\partial B_{r}(\textbf{0})$ de la bola $B_{r}(\textbf{0})$ es una circunferencia generalizada del plano complejo extendido $\widehat{\mathbb{C}}.$ Del Teorema 2, existe una circunferencia $C$ sobre la esfera $\mathbb{S}^2$ cuya imagen bajo $\Pi$ es la frontera $\partial B_{r}(\textbf{0}).$ Por construcción, la esfera $\mathbb{S}$ menos la circunferencia $C$ es la unión disjunta de dos abiertos conexos, tal que uno de ellos contiene el polo norte ${\rm N}.$ Denotemos mediante $W$ a dicha componente conexa que contine a ${\rm N}.$ Dado que $\Pi$ es continua en $\mathbb{S}^{2}-\{\rm N\},$ entonces debe suceder que $\Pi(W)\subset V.$ Esto prueba que la proyección estereográfica $\Pi$ es continua en ${\rm N}.$ Por lo tanto, la proyección estereográfica es continua en $\mathbb{S}^{2}.$

Recordemos que toda función continua definida desde un espacio compacto hasta un espacio Hausdorff es cerrada (véase Dugundji, 2.1 Theorem, pág. 226). Usando el anterio hecho, concluimos que la proyección estereográfica $\Pi$ es una función cerrada. Como la proyección estereográfica $\Pi$ es una función biyectiva, continua y cerrada, entonces concluimos que en efecto es un homeomorfismo.

La métrica usual de $\mathbb{R}^3,$ la cual está dada mediante

\[ \left|(x_1,x_2,x_3)-(y_1,y_2,y_3)\right|:=\sqrt{\sum\limits_{i=1}^3(x_i-y_i)^2}, \]

para cualesquiera elementos $(x_1,x_2,x_3),(y_1,y_2,y_3)\in \mathbb{R}^3$ la podemos restringir a la esfera de Riemann $\mathbb{S}^2.$ Mediante la proyección estereogr'afica $\Pi$ podemos definir en el plano complejo extendido $\hat{\mathbb{C}}$ la función distancia $d_c : \hat{\mathbb{C}}\times \hat{\mathbb{C}} \to \mathbb{R}$ tal que

\[ d_c(z,w)=\left|\Pi^{-1}(z)-\Pi^{-1}(w)\right|= \left\{ \begin{array}{ ll } \dfrac{2|z-w|}{\sqrt{1+|z|^2}\sqrt{1+|w|^2}}; & \text{ si } z,w\neq \infty; \\ \dfrac{2}{\sqrt{1+|z|^2}}; & \text{ si } w=\infty.\\ \end{array} \right. \]

A esta función distancia se le conoce como métrica cordal -cuerdas-, pues geométricamente esta distancia representa la longitud del segmento en $\mathbb{R}^3$ con puntos extremos $\Pi^{-1}(z)$ y $\Pi^{-1}(w).$ Adicionalmente, la topología inducida por la métrica cordal es equivalente a la topología $\tau_{\infty}.$

Plano Proyectivo Complejo

Plano Proyectivo Complejo $\mathbb{C}P^{1}$

La esfera de Riemann se puede enteder como $\mathbb{C}^{2}\setminus \{(0,0)\}$ módulo una adecuada relación de equivalencia. Este espacio cociente es conocido como el Plano Proyectivo Complejo $1$ dimensional. Este objeto es estudiado desde la perspectiva de las curvas algebraicas.

En adelante $\mathbb{C}^{\ast}$ denotará a los números complejos removiendo el $0.$ El conjunto $\mathbb{C}^{\ast}$ actúa sobre $\mathbb{C}^2-\{(0,0)\}$ por multiplicación, es decir, la función

$$ \alpha: \mathbb{C}^{\ast}\times \mathbb{C}^{2}\setminus\{(0,0)\}\to \mathbb{C}^{2}\setminus\{(0,0)\} $$

dada por \begin{equation}\label{eq:accion_plano_proyectivo_complejo} (\lambda, (z,w))\to (\lambda\cdot z, \lambda\cdot w), \end{equation} es una acción, donde $\cdot$ es la multiplicación compleja usual. Entonces el espacio cociente \[ \mathbb{C}^{2}-\{(0,0)\}/\mathbb{C}^{\ast}, \] es llamado espacio proyectivo complejo $1$-dimensional. Formalmente, lo podemos introducir como sigue.

El espacio proyectivo complejo $1$-dimensional es el espacio

\[ \mathbb{C}P^{1}:=\mathbb{C}^{2}-\{(0,0)\}/\mathbb{C}^{\ast}=\left\{(z,w)\in\mathbb{C}^{2}-\{(0,0)\}\right\}/\sim, \]

donde $\sim$ es la relación de equivalencia: $(z_1,w_1)\sim (z_2,w_2)$ si y solo si existe $\lambda \in\mathbb{C}^{\ast}$ tal que $(z_1,w_1)=(\lambda \cdot z_2,\lambda \cdot w_2).$ El espacio $\mathbb{C}P^{1}$ está dotado con la la topología identificación, es decir, la topología que hace a la función proyección $p:\mathbb{C}^{2}-\{(0,0)\}\to \mathbb{C}P^{1},$ tal que \[ (z,w)\mapsto [z,w], \] continua.

Notemos que $\mathbb{C}P^{1}$ está conformado por todos los subespacios vectoriales complejos de dimensión $1$ en $\mathbb{C}^2.$ El siguiente resultado describe algunas de las propiedades topológicas de este plano proyectivo complejo.

El plano proyectivo complejo $1$-dimensional $\mathbb{C}P^1$ es un espacio compacto, conexo y Hausdorff.

Notemos que la esfera compleja

\[ \mathbb{S}^{3}:=\left\{(z,w)\in\mathbb{C}^2: |z|^2+|w|^2=1\right\}\subset \mathbb{C}^2-\{(0,0)\}, \]

es un espacio compacto y conexo.

Dado que la función inclusión $i:\mathbb{S}^3\hookrightarrow \mathbb{C}^2-\{(0,0)\}$ es continua y la composición de funciones continuas es continuas, entonces la función composición $p\circ i:\mathbb{S}^3\to\mathbb{C}P^{1}$ es continua. Si probamos que $i\circ p$ es sobreyectiva, podremos concluir que $\mathbb{C}P^{1}$ es un espacio compacto y conexo, pues estas dos propiedades son invariantes bajo continuidad. Tomemos la clase $[z,w]\in \mathbb{C}P^{1},$ como alguna de sus entradas es no nula, entonces definimos el número complejo no nulo \[ \lambda =|z|^2+|w|^2\neq 0. \] Notemos que la pareja $(z/\lambda,w/\lambda)$ pertenece a la esfera compleja $\mathbb{S}^3$ y es equivalente a la pareja $(z,w)\in \mathbb{C}^{2}\setminus\{(0,0)\}.$ Esto implica que $p\circ i (z/\lambda,w/\lambda)=[z,w].$

Finalmente, vamos a probar que $\mathbb{C}P^{1}$ es un espacio Hausdorff. El siguiente conjunto es necesario para la prueba. Dado el subconjunto abierto $U\subset \mathbb{C}^{2}\setminus \{(0,0)\}$ y el complejo no nulo $\lambda\in\mathbb{C}^{\ast},$ definimos el transladado de $U$ con respecto a $\lambda$ como el abierto

\begin{equation}\label{eq:transladado_abierto} \lambda \cdot U=\left\{(\lambda\cdot z,\lambda \cdot w): (z,w)\in U\right\}. \end{equation}

Ahora, tomemos dos puntos diferentes $[z_1,w_1]\neq [z_2,w_2]\in\mathbb{C}P^{1}.$ Podemos suponer sin pérdida de generalidad que $(z_1,w_1),$$(z_2,w_2)\in \mathbb{S}^{3}.$ Dado que $\mathbb{S}^{3}$ es un espacio Hausdorff, entonces existen abiertos $U$ y $V$ en $\mathbb{S}^{3}$ tal que se satisfacen las siguientes propiedades

El punto $(z_1,w_1)$ está en $U$ y el punto $(z_2,w_2)$ está en $V.$
La intersección $U\cap V=\emptyset.$

Por otro lado, tenemos que las imágenes $p\circ i(U)$ y $p\circ i(V)$ satisfacen:

La clase $[z_1,w_1]$ está en $p\circ i(U)$ y la clase $[z_2,w_2]$ está en $p\circ i(V).$
Los subconjuntos $p\circ i(U)$ y $p\circ i(V)$ son abiertos en $\mathbb{C}P^{1},$ dado que
\[ p^{-1}(p(U))=\bigcup_{\lambda\in\{1,-1\}} \lambda \cdot U \text{ y } p^{-1}(p(V))=\bigcup_{\lambda\in\{1,-1\}} \lambda \cdot V. \]
La intersección $p\circ i(U)\cap p\circ i(V)\neq \emptyset.$

Esto prueba que el espacio $\mathbb{C}P^{1}$ es Hausdorff.

Para finalizar esta sección el lector tendrá la tarea de probar que la función $f:\mathbb{C}P^{1}\to\mathbb{S}^2,$ definida mediante

\begin{equation}\label{eq:homeo_esfera_plano_proyectivo} [z,w]\mapsto \left(\frac{2Re(z\overline{w})}{|z|^2+|w|^2},\frac{2Im(z\overline{w})}{|z|^2+|w|^2},\frac{|z|^2-|w|^2}{|z|^2+|w|^2}\right), \end{equation}

es un homeomorfismo.

Problemas

Probar la afirmación (ii) descrita en el Teorema 1.
Demostrar que la esfera de Riemann $\widehat{\mathbb{C}}$ es un espacio conexo, segundo numerable y normal.
Verificar que la distancia $D$ desde un punto arbitrario $(x_{0},y_{0},z_{0})\in\mathbb{R}^{3}$ hasta el plano $P$ con ecuación $ax_{1}+bx_{2}+cx_{3}=d,$ está dada por la fórmula \[ D=\dfrac{|ax_{0}+by_{0}+cz_{0}-d|}{\sqrt{a^{2}+b^{2}+c^{2}}}. \]
Probar que la función que define la métrica cordal, es en efecto una función distancia. Verifica que la topología inducida por la métrica cordal es equivalente a la topología $\tau_{\infty}.$
Para todo $n\in\mathbb{N},$ demostrar que el espacio $\mathbb{R}^n\cup\{\infty\}$ con la topología $\tau_{\infty}$ es homeomorfo a
$$\mathbb{S}^{n}:=\left\{(x_1,\ldots,x_{n+1})\in \mathbb{R}^{n+1}: \sqrt{\sum\limits_{i=1}^{n+1}x_i^2}=1\right\}.$$
Verificar que la función $\alpha$ definida en la ecuación \eqref{eq:accion_plano_proyectivo_complejo} es una acción.
Probar que el abierto transladado $\lambda \cdot U$ definido en la ecuación \eqref{eq:transladado_abierto} es un abierto.
Demostrar que la función $f:\mathbb{C}P^{1}\to\mathbb{S}^2,$ definida mediante
\[ [z,w]\mapsto \left(\frac{2Re(z\overline{w})}{|z|^2+|w|^2},\frac{2Im(z\overline{w})}{|z|^2+|w|^2},\frac{|z|^2-|w|^2}{|z|^2+|w|^2}\right), \]
es un homeomorfismo.